November 9, 2023

From the 2021 UPC Illustrated Training Manual, Chapter 11, STORM DRAINAGE
1103.4 Side Walls Draining onto a Roof. Where vertical walls project above a roof to permit storm water to drain into the roof area below, the adjacent roof area shall be permitted to be computed from Table 1103.1 as follows:
In determining this maximum horizontal projected roof area the user is calculating the area of roof that rain may fall upon and the amount of rainwater demand, calculated in square feet, it creates. But this is not the only area that contributes to the amount of rainwater on the roof. As rain falls it rarely falls in a direct vertical line to the ground. Wind normally accompanies rain and causes the rain to fall at an angle to the ground. If there are side walls projecting vertically up from the roof, they will block the rainfall and cause it to drain onto the roof. This causes an increase in the amount of rainwater that can collect on the roof. These contributing, or “tributary,” areas must be added to the total projected roof area and be represented in square feet so that one can easily determine the size of the roof drain and piping. To accomplish this, Section 1103.4 contains the parameters to determine the square foot area to be added to the maximum horizontal projected roof area for the seven different side-wall conditions that may occur.
Although there are seven conditions discussed here, there are only two percentages that must be used to calculate the total roof area. The first percentage is for a wall that is above other walls on a roof, or a wall that stands alone and is not adjacent or opposite other walls. Fifty percent of this wall area is added to the flat area of the roof. This factor takes into consideration that the wall does not collect rainfall as a flat area would; thus, only half of the area of the wall needs to be added to the total area of the roof. The second percentage is for adjacent or connecting side walls. Thirty-five percent of the total wall area of both walls is added to the projected roof area. This factor takes into consideration the fact that one connecting wall will block a portion of the rainfall from falling on the other wall. Thus, only 35 percent of both wall areas are added to the total area of the roof.
For the following examples, the flat area of the roof will be given 500 ft2, and the typical wall area represented by each wall segment will be given a height of 10 feet with a width of 20 feet, which is 200 ft2.
(1) For one wall – add 50 percent of the wall area to the roof area figures.

In Example 1, a single wall projecting above the roof would add 50 percent of the total area of the wall or 100 ft2 to the flat area of the roof. The total projected roof area would then be 600 ft2. This amount would then be used this to determine the size of the horizontal drain, conductor, or gutter.
(2) For two adjacent walls of equal height – add 35 percent of the total wall areas.
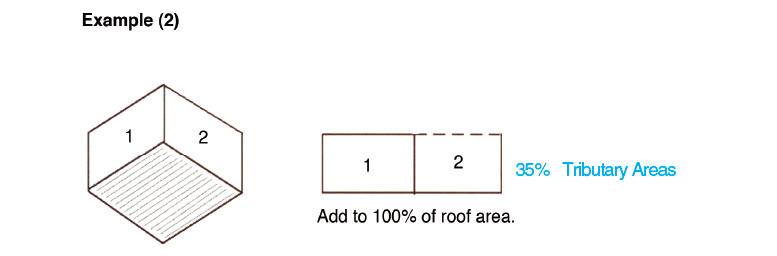
In Example 2, using the same square footage as above, there are two walls of equal height with the sum of 400 ft2. Because the walls are adjacent – next to each other rather than opposite each other – only 35 percent of the 400, which is 140 ft2 will be used in the total square feet. The total projected roof area of 640 ft2 would then be used to determine the size of the horizontal drain, conductor or gutter.
In computing the area of adjacent walls of equal height, it has been determined that all of the wall area of the adjacent walls, whether one wall is longer than the other or not, should be used and computed at 35 percent. For example, if one of the walls above was 30 feet wide, the computation would be: 10 x 30 = 300 + (10×20) = 500 x 35% = 175 ft2.
(3) For two adjacent walls of unequal height – add 35 percent of the total common height and add 50 percent of the remaining height of the highest wall.

In computing the area of adjacent walls of unequal height, use the method used in Example 2 for the adjacent wall area that is of equal height. The remaining wall area above the area of equal height will be calculated as in Example 1.
In Example 3, the two adjacent areas of equal height (wall sections 1a and 2) are calculated as follows: (10 x 20) + (10 x 20) = 400 ft2 x 35% = 140 ft2. The area above the equal height walls (wall section 1b), 10 x 20 = 200 ft2, would be calculated at 50 percent, which is 100 ft2. Add this to 140 ft2 for a total of 240 ft2. The total projected roof area of 740 ft2 would then be used to determine the size of the horizontal drain, conductor, or gutter.
(4) Two opposite walls of same height – add no additional area.

In Example 4, two opposite walls of the same height will “cancel” each other. One wall will catch rain adding to the rainwater on the roof, while the other wall will block the same amount of rain from falling on the roof. Therefore, no area is added to the 500 square feet of flat roof area.
(5) Two opposite walls of differing heights – add 50 percent of the wall area above the top of the lower wall.
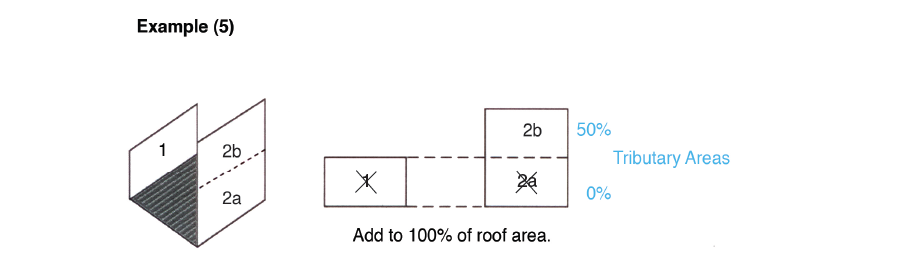
As in Example 4 so also in Example 5 the two opposite walls of the same height will cancel each other (wall sections 1 and 2a). Wall section 2b is higher than the other wall, and is calculated as if it was a wall by itself – no wall opposite and no wall adjacent. Therefore, 50 percent of the area of wall section 2b is added to the flat roof area. Using the same numbers (10 x 20 x 50%) would add 100 ft2 to the total flat roof area of 500 ft2 for a total of 600 ft2 of projected roof area. This amount would then be used to determine the size of the horizontal drain, conductor, or gutter.
(6) Walls on three sides – add 50 percent of the area of the inner wall below the top of the lowest wall, plus an allowance for the area of the wall above the top of the lowest wall, in accordance with Section 1103.4(3) and Section 1103.4(5) above.

For Example 6, in order to determine the computation of the square footage that is added to the total projected roof area for three walls of differing heights, use the same criteria as in the previous examples. Per Example 4, the two opposite walls (wall sections 1 and 3a) cancel each other. Per Example 1, the inner wall (wall section 2a) will be calculated as one wall (since wall sections 1 and 3a have been cancelled) at 50 percent, or 100 ft2 (as in Example 1 above). Wall sections 2b and 3b are adjacent walls of equal height and will be calculated as Example 3 at 35 percent, or 140 ft2. Wall section 3c will be calculated as Example 3 as a wall section above adjacent walls at 50 percent, or 100 ft2. A total of 340 ft2 must be added to the 500 ft2 flat roof projected area for a total of 840 ft2. This amount would then be used to determine the size of the horizontal drain, conductor, or gutter.
(7) Walls on four sides – no allowance for wall areas below the top of the lowest wall – add for areas above the top of the lowest wall in accordance with Section 1103.4(1), Section 1103.4(3), Section 1103.4(5), and Section 1103.4(6) above.

For Example 7, in order to determine the computation of the square footage to be added to the total projected roof area for four walls of differing heights, use the same criteria as in the previous examples. Wall sections 1, 2a, 3a, and 4a are of the same height and opposite each other, and therefore will cancel each other as in Example 4. For wall sections 2b and 4b, the two are opposite walls and cancel each other. Wall section 3b will be computed as one wall standing alone at 50 percent, or 100 ft2 per Example 1. Wall sections 3c and 4c are adjacent walls of equal height and will be computed at 35 percent, or 140 ft2, as Example 2. Wall section 4d will be computed at 50 percent, or 100 ft2, as Example 3. Therefore, a total of 340 ft2 will be added to the 500 ft2 “flat” roof projected area for a total of 840 ft2. This amount would then be used to determine the size of the horizontal drain, conductor, or gutter.
Although roof drainage sizing may seem complicated it can be very simple. Just remember that if the wall is standing alone or above the other walls add 50 percent of the wall area to the “flat” area of the roof. If the walls are adjacent add 35 percent of the wall area to the “flat” area of the roof. And if the walls are opposite and of equal height they cancel each other.
The 2021 Uniform Plumbing Code Illustrated Training Manual is available for purchase here.
(This is not to be considered the official position of IAPMO, nor is it an official interpretation of the Codes.)

IAPMO
IAPMO develops and publishes the Uniform Plumbing Code®,the most widely recognized code of practice used by the plumbing industry worldwide; Uniform Mechanical Code®; Uniform Swimming Pool, Spa and Hot Tub Code®; and Uniform Solar Energy, Hydronics and Geothermal Code™ — the only plumbing, mechanical, solar energy and swimming pool codes designated by ANSI as American National Standards — and the Water Efficiency Standard (WE-Stand)™. IAPMO works with government, contractors, labor force, and manufacturers to produce product standards, technical manuals, personnel certification/educational programs and additional resources in order to meet the ever-evolving demands of the industry in protecting public health and safety.
Last modified: November 9, 2023
